Attention is all I need：Transformer的原理和代码详解

Transformer可运行的代码发布在GitHub

提到ChatGPT的原理，就绕不开Transformer，Transformer中的核心思想之一便是Attention，Attention机制彻底击败了在此之前的绝对王者RNN模式，并统治各大NLP任务直到现在。正因如此，Transformer的论文不叫Transformer，而是叫做《Attention is all you need》。本文是以我的理解，阐述Transformer是怎么想出来的，为什么这么设计。

Attention的思想

Attention的关键在于理解$QKV$，即Query、Key和Value。可以将Attention机制看作一种寻址操作：存储器中存有键Key和值Value，当前产生了一个Query的查询，要查询出Value，那么首先需要匹配Query和Key的相似度。举个也许不恰当，但直观的例子，有以下Key和Value：

Key	Value
段誉的招牌武功	六脉神剑
段誉的生父	段延庆
段誉的结拜兄弟	乔峰和虚竹
乔峰的招牌武功	降龙十八章

寻址流程如下：

发起Query：“段誉的生父是谁？”
与Key相似度匹配到“段誉的生父”
返回Value“段延庆”

这里的关键是相似度计算方法，通常是Query和Key的矩阵乘法，或加个缩放$\sqrt{d_k}$，或乘个$W$，如下：

矩阵相乘：$sim(Q,K)=QK^T$
相乘加缩放：$sim(Q,K)=\frac{QK^T}{\sqrt{d_k}}$（Transformer使用，缩放使得训练可以收敛）
权重+激活：$sim(Q,K)=tanh(WQ+UK)$
权重+相乘：$sim(Q,K)=QWK^T$

取出一个或者部分Value的方法叫Hard Attention，如上例只输出“段延庆”。但是，如果我问“段誉结拜兄弟的招牌武功是什么？”，Hard Attention可能匹配到“段誉的结拜兄弟”，输出“乔峰和虚竹”，这就不对了。替代方案就是Soft Attention，提供所有Value和对应的Attention权重，当$Q=$“段誉结拜兄弟的招牌武功是什么？”，结果可能如下表：

Key	Attention权重	Value
段誉的招牌武功	7	六脉神剑
段誉的生父	1	段延庆
段誉的结拜兄弟	9	乔峰和虚竹
乔峰的招牌武功	5	降龙十八章

这样，就可以把高分答案结合，得到正确答案。当问题更宏大，需要的信息就更多，于是干脆每次都输出整张表，虽然有可能冗余，但这样得到的答案是既有重点、又完整的。

以往设备限制导致计算和输出全部非常困难，但现在设备的发展使得超大规模、超长文本输入的LLM得以出现，而Transformer的self-attention保证了LLM的效率和学习能力。

Self-Attention

Self-Attention说来很简单，就是$Q=K=V$。

为什么要这么做？个人理解是让一句话先找出自己内部的关键词，再去适配下游的任务。例如$Q=K=V=青花瓷$，用Pytorch简单计算如下：

  
from torch import nn as nn
import torch
# {青:0, 花:1, 瓷:2}
tokens = torch.LongTensor([0, 1, 2])
# 将3个字转换成向量，向量维度为10
token_embedding = nn.Embedding(3, 10)
emb = token_embedding(tokens)
# 相似度计算
QK = torch.mm(emb, emb.T) / torch.sqrt(torch.FloatTensor([10]))
print(QK)

由于nn.Embedding随机初始化，所以结果会不一样，我的结果表述如下：

\[sim(Q,K)= \begin{bmatrix} 青 & 花 & 瓷 \end{bmatrix} \times \begin{bmatrix} 青\\ 花\\ 瓷 \end{bmatrix} /10 = \begin{bmatrix} 3.2897 & 0.7432 & -1.1652 \\ 0.7432 & 1.3647 & -1.1707\\ -1.1652 & -1.1707 & 5.6380 \end{bmatrix}\]

矩阵对角线表示自身的相似度，比如3.2897就表示“青”和“青”的相似度，就很大。每行代表每个字的权重。由于点积可以产生任意大的数字，这会破坏训练过程的稳定性，因此需要 $Softmax$。Attention的公式表示为：

\[\text{Attention}(Q, K, V) = \text{Softmax} \big( \frac{QK^T}{\sqrt{d_k}} \big)V\]

代码只须再加上：

  
Attention = torch.mm(torch.softmax(QK, dim=-1), emb)

这样得到矩阵的每行就表示[青, 花, 瓷]这三个字的Attention。在训练过程中会更新这些参数，从而根据上下文和标签得到更好的向量表示。

Multi-head Attention

为了关注到更多信息，Transformer采用Multi-head Attention机制，也就是重复n次Attention操作然后拼接，得到和原来的Attention维度相同的MultiHead，公式为：

\[\begin{gather}head_i = \text{Attention}(\boldsymbol{Q}\boldsymbol{W}_i^Q,\boldsymbol{K}\boldsymbol{W}_i^K,\boldsymbol{V}\boldsymbol{W}_i^V)\\\text{MultiHead}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = \text{Concat}(head_1,...,head_h)\boldsymbol{W}^O\end{gather}\]

其中 $\boldsymbol{W}_i^Q\in\mathbb{R}^{d_{model}\times d_k}, \boldsymbol{W}_i^K\in\mathbb{R}^{d_{model}\times d_k}, \boldsymbol{W}_i^V\in\mathbb{R}^{d_{model}\times d_v},\boldsymbol{W}^O\in\mathbb{R}^{hd_{v}\times d_{model}}$ 。

原文模型的维度$d_{model}$是512，我们设置$h=8$个注意力头，那么$d_k=d_v=d_{model}/h=64$。每个注意力头负责关注某一方面的语义相似性，多个头就可以让模型同时关注多个方面。不怎么严谨的代码如下，便于理解：

  
from torch import nn
import torch.nn.functional as F
from math import sqrt
import torch

class AttentionHead(nn.Module):
    def __init__(self, embed_dim, head_dim):
        super().__init__()
        self.WQ = nn.Linear(embed_dim, head_dim)
        self.WK = nn.Linear(embed_dim, head_dim)
        self.WV = nn.Linear(embed_dim, head_dim)

    def forward(self, query, key, value):
        QK = torch.mm(WQ(query), WK(key).T) / torch.sqrt(query.size(-1))
        Attention = torch.mm(torch.softmax(QK, dim=-1), WV(value))
        return Attention
    
class MultiHeadAttention(nn.Module):
    def __init__(self, config):
        super().__init__()
        embed_dim = config.hidden_size
        num_heads = config.num_attention_heads
        head_dim = embed_dim // num_heads
        self.heads = nn.ModuleList(
            [AttentionHead(embed_dim, head_dim) for _ in range(num_heads)]
        )
        self.output_linear = nn.Linear(embed_dim, embed_dim)

    def forward(self, query, key, value):
        MultiHead = torch.cat([h(query, key, value) for h in self.heads], dim=-1)
        x = self.output_linear(MultiHead)
        return x

更多时候，为了并行效率，多头操作是先乘上$\boldsymbol{W}\in\mathbb{R}^{d_{model}\times d_{model}}$的权重矩阵，再将QKV切块相乘，同一个结果但是抛弃了for循环，我的仓库中就是这种做法。Transformer最核心的就是上文所述的Attention，下面介绍其他部分。

Encoder-Decoder

之前的博客介绍了Encoder-Decoder结构，Transformer也遵从这种结构。而Transformer“浑身都是宝”，每个部分都被开发出了作用：

Transformer的Encoder（如BERT），又称自编码 (auto-encoding) Transformer 模型
Transformer的Decoder（如GPT系列），又称自回归 (auto-regressive) Transformer 模型
完整的Encoder-Decoder（例如BART、T5等）

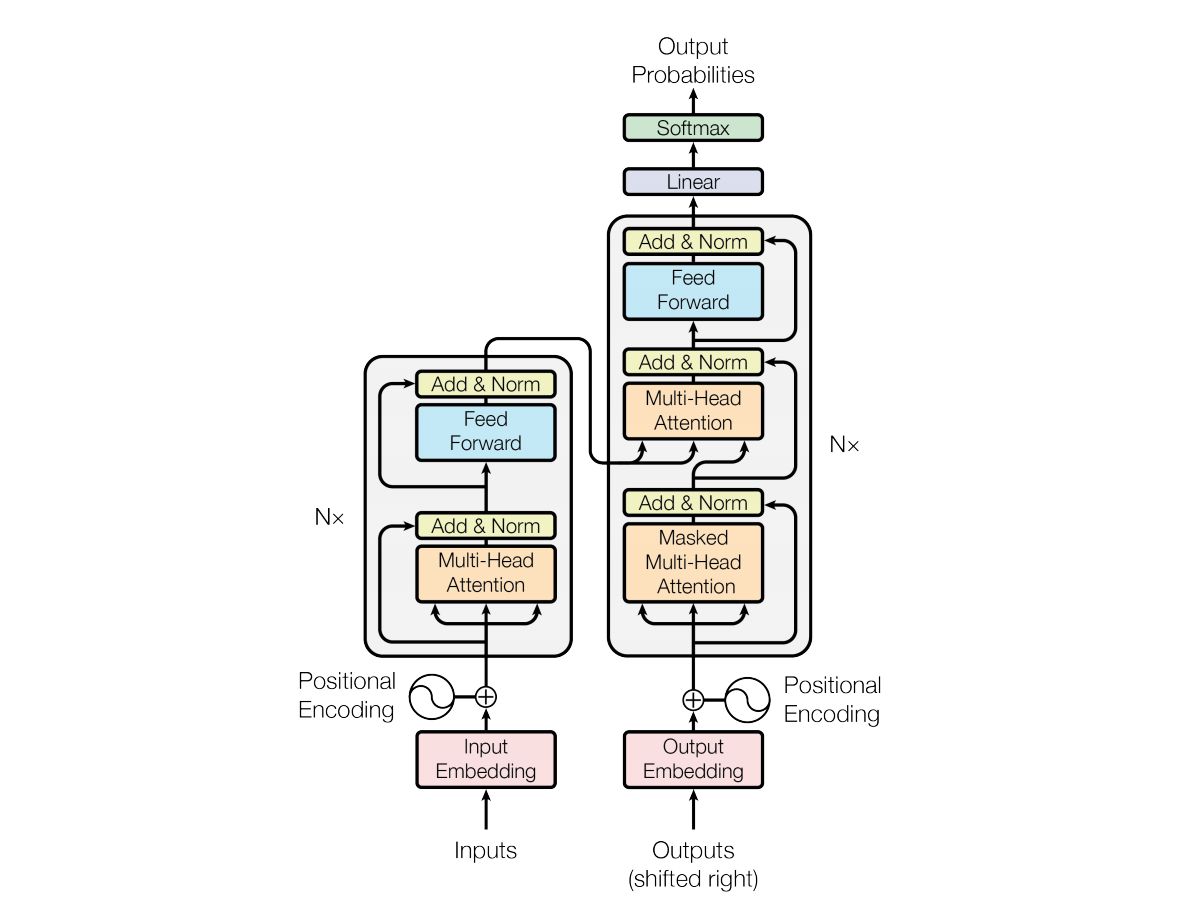
理解了Transformer，以上模型的上手难度会小很多，我们之后再了解。Transformer整体结构如图：

左边是Encoder，右边是Decoder，可以看到两边都有：

Positional Encoding
Multi-head Attention
Feed Forward
Add & Norm。

Multi-head Attention已经在上文介绍了，介绍下其他几位。

Positional Encoding

在Attention中其实可以看出，并没有任何有关位置的特征，这样”一步两步三步四步望着天“的每一个”步“向量都是一样的，甚至把这句话变成”天着望步四步三步两步”一“，都是一样的，这显然不合理。因为每一步情绪都是递进的，而Attention无法解决前后顺序和句子内的一词多义。

RNN通过记忆使得每一步不一样，而Transformer采用了Positional Encoding，即位置编码，其公式如下：

\[\begin{gather} PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})\\ PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}}) \end{gather}\]

意思就是向量的偶数位置填$sin$，奇数位置填$cos$，$pos$指相对位置，如”青花瓷“的”青“的$pos$就是0。对”青花瓷“这三个10维的向量进行位置编码，简单实现代码如下：

  
import math
import torch

seq_len = 3
d_model = 10
pe = torch.zeros(seq_len, d_model)
position = torch.arange(0, seq_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
                     -math.log(10000.0) / d_model)
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
print(pe)

由于次方比较难算，利用$e^{lnx}=x$的性质，代码中进行了如下转换：

\[\frac{1}{10000^{2i/d}} =e^{ln\frac{1}{10000^{2i/d}}} =e^{-\frac{2i}{d}ln10000}\]

得到的PE矩阵用来加上原始的词向量。位置编码相当于根据位置给权重。为什么这么做？我们从0开始思考，让我设计位置编码，怎么设计？

\[一步两步三步四步望着天:[0,1,2,3,4,5,6,7,8,9,10]\]

问题在哪？跟embedding向量的数字相比，这个数字太大了，那归一化一下：

\[一步两步三步四步望着天:[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1]\]

这样的问题在于无法体现位置关系，因为注意力是相乘，下面采取相乘：$0.1 \times 1=0.2 \times 0.5$，不同距离相乘居然一样，反之，相同距离相乘居然不一样。大概有头绪了，位置编码起码需要满足这些条件：SSS

相同距离相乘一样；
不同距离相乘不一样；
数量不限：序列无论多长都能找到相应的位置编码表示。

Transformer本身是加入额外的位置，词向量加上位置的绝对位置编码。另外，还有修改Attention结构的相对位置编码。而下面介绍苏神的Rope结合了两者。

Rope位置编码

根据Transformer的位置编码公式，$pos+k$位置的编码如下：

\[\begin{gather} PE_{(pos+k,2i)}=sin((pos+k)/10000^{2i/d_{model}})\\ PE_{(pos+k,2i+1)}=cos((pos+k)/10000^{2i/d_{model}}) \end{gather}\]

先令$w_i=1/10000^{2i/d_{model}}$，根据：

\[\begin{gather} sin(\alpha+\beta)=sin\alpha \cdot cos\beta+cos\alpha \cdot sin\beta\\ cos(\alpha+\beta)=cos\alpha \cdot cos\beta-sin\alpha \cdot sin\beta \end{gather}\]

推导出：

\[\begin{gather} PE_{(pos+k,2i)}=sin(w_i(pos+k))=sin(w_ipos) \cdot cos(w_ik)+cos(w_ipos) \cdot sin(w_ik)\\ PE_{(pos+k,2i+1)}=cos(w_i(pos+k))=cos(w_ipos) \cdot cos(w_ik)-sin(w_ipos) \cdot sin(w_ik) \end{gather}\]

就是多了$k$的部分，可以表示为矩阵：

\[\begin{bmatrix} PE_{(pos+k,2i)} \\ PE_{(pos+k,2i+1)} \end{bmatrix} = \begin{bmatrix} cos(w_ik) & sin(w_ik) \\ -sin(w_ik) & cos(w_ik) \end{bmatrix} \times \begin{bmatrix} PE_{(pos,2i)} \\ PE_{(pos,2i+1)} \end{bmatrix}\]

令:

\[R_k= \begin{bmatrix} cos(w_ik) & sin(w_ik) \\ -sin(w_ik) & cos(w_ik) \end{bmatrix}^T\]

根据：

\[\begin{gather} -sinx=sin-x \\ cosx=cos-x \end{gather}\]

易得：

\[R_k = R_{-k}^T\]

并有如下性质，从而可以表示相对位置：

\[R_{k_2-k_1}=R_{k_1}^TR_{k_2}\]

对位置为$m$的词向量$A$和位置为$n$的$B$，对他们乘上$R_m$和$R_n$，就给Attention加上了绝对位置信息，并且具有$m-n$的相对位置信息：

\[AR_m(BR_n)^T=AR_mR_n^TB=AR_{n-m}B\]

Rope被许多大模型如LLaMA、falcon等采用。以往较多模型采用直接embedding+学习的方式，但是这样最开始就定死了长度，遇到长文本只能截断，而Rope改良了这一点，使得大模型具有处理超长文本的能力。更多位置编码方式，可以参考苏神的博客《让研究人员绞尽脑汁的Transformer位置编码》。

Feed Forward

Feed Forward简称FFN，在Encoder和Decoder的压轴处都各有一层，由两个全连接和ReLU激活函数组成，如下式：

\[FFN(X)=max(0,xW_1+b_1)W_2+b_2\]

这个$max$就是ReLU。各个激活函数如图：

ReLU的导数只有0和1，使得计算成本很低。

两层全连接把模型维度从512扩展到了2048又回到512。我找遍了原文和各个教程，都没有详细解释这一步的作用。

个人理解可能是扩展到更高维度以储存更多信息，但之前这么多参数还不够？

也可能是加个激活函数，但是之前也有Softmax。

有加入类似层进行调参的工作：adapter，但其真实设计意图是什么，也不得而知了。

Add & Norm

Add & Norm由Add和Norm两部分组成。

Add是将箭头指过来的两者相加，包括Attention和原embedding这两个矩阵相加、以及过了FFN和没过之前的矩阵相加，这个很简单，就不细说了。

Norm指标准化，Transformer中使用LayerNorm，在图像领域常使用BatchNorm，两者都是拿均值方差做标准化处理，都是下式：

\[y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon }}\]

其中$E[x]$为均值，$Var[x]$为方差，$\epsilon$是一个很小的常数，用于避免分母为零。区别就在于两者拿来算均值方差的数不一样，如下：

LayerNorm的均值方差，是对单个样本的不同特征做操作，即每个词向量内部；
BatchNorm是对不同样本的同一特征做操作。

拿“青花瓷”的相似矩阵为例，手推LayerNorm：

  
import torch.nn as nn
import math
matrix = torch.Tensor([[3.2897, 0.7432, -1.1652],
                       [0.7432, 1.3647, -1.1707],
                       [-1.1652, -1.1707, 5.6380]])
# torch官方的layer_norm
layer_norm = nn.LayerNorm(matrix.shape[-1])
y_torch = layer_norm(matrix)
print(y_torch)
# 初始化一个与matrix大小相同的全0矩阵
y_ours = torch.zeros_like(matrix)
# 手推均值方差和LayerNorm
for row in range(matrix.shape[0]):
    E = sum(matrix[row]) / len(matrix[row])
    Var = 0
    for col in range(matrix.shape[1]):
        Var += (matrix[row, col] - E) ** 2 / len(matrix[row])
    for col in range(matrix.shape[1]):
        y_ours[row, col] = (matrix[row, col] - E) / math.sqrt(Var + 1e-5)
print(y_ours)

求得的结果是一样的。可以看到结果中，有小于0也有大于1的，因此我认为有些教程称之为“归一化”是不合理的，归一化是通过MinMax将所有数据转换至0-1范围内。而LayerNorm，明显是均值0方差1的标准化。

BatchNorm的代码如下：

  
import torch.nn as nn
import math
matrix = torch.Tensor([[3.2897, 0.7432, -1.1652],
                       [0.7432, 1.3647, -1.1707],
                       [-1.1652, -1.1707, 5.6380]])
layer_norm = nn.BatchNorm1d(matrix.shape[-1])
y_batch = layer_norm(matrix)
print(y_batch)
y_ours = torch.zeros_like(matrix)
# 手动求均值方差和norm
for col in range(matrix.shape[1]):
    E = sum(matrix[:, col]) / len(matrix[:, col])
    Var = 0
    for row in range(matrix.shape[0]):
        Var += (matrix[row, col] - E) ** 2 / len(matrix[row])
    for row in range(matrix.shape[1]):
        y_ours[row, col] = (matrix[row, col] - E) / math.sqrt(Var + 1e-5)
print(y_ours)

差别就在于LayerNorm在行，BatchNorm在列。

Transformer 为什么使用 Layer？这个问题还没有啥定论，包括LN和BN为啥能work也众说纷纭，感兴趣的话可以参考原文和以下论文：

PowerNorm: Rethinking Batch Normalization in Transformers [1]
Understanding and Improving Layer Normalization [2]

了解Transformer这些基本组件后，还有值得探讨的是Mask。

Transformer中的Mask

此Mask非彼BERT的的那个掩码Mask。这里的Mask指Pad Mask和Attention Mask。

在Encoder中，Pad Mask需要去掉$<pad>$的计算。什么是$<pad>$呢？为了并行计算提高训练速度，通常把数据打包成batch，一批批训练，例如一个batch：

[“青花瓷”, “爱在西元前”, “星晴”]

但是模型只能处理长度相同的句，于是用<pad>填充到相同长度

[“青花瓷$<pad><pad>$”, “爱在西元前”, “星晴$<pad><pad><pad>$”]

计算时把$<pad>$的位置设置成负无穷，softmax的值就趋于0，从而忽略。

在Decoder中同样要Pad Mask，除此之外还需要Attention Mask来遮住后面的词。例如训练时文本是“星晴”，标签是“乘着风”，虽然知道标签全句“乘着风”，但是推理时是一个词一个词预测的，Decoder预测出“乘”时，并不知道后面是“着风”。为了在训练时适配推理，预测“着”时需要把“着风”给Mask，也就是去掉“乘”与“着”、“风”的相似度。

”乘着风$<pad><pad>$“的Attention Mask矩阵如图：

\[\begin{matrix} 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 & 0\\ 1 & 1 & 1 & 0 & 0\\ 1 & 1 & 1 & 0 & 0\\ 1 & 1 & 1 & 0 & 0\\ \end{matrix}\]

对应相似度矩阵0的位置会被替换成负无穷，softmax后值就趋于0，从而使得Attention矩阵第一行就只有第一个字的权重，第二行有一二两个字的权重，以此类推。

Transformer全览

结合上述所有组件，对照着模型图，对Transformer做个全览。

Encoder的流程如下：

输入是“星晴”，先根据词表转化为2个向量的矩阵
加上位置信息
过Self-Attention
和没过Self-Attention的矩阵相加，然后LayerNorm标准化
过FFN，再和没过FFN的矩阵相加，然后LayerNorm标准化
得到跟输入向量维度一样的Encoder矩阵

为了告诉Decoder从哪开始到哪结束，需要添加开始符和结束符，例如$<sos>$（start of sentence）和$<eos>$（end of sentence）。Decoder训练的流程如下：

标签是$\text{trg} = [sos, x_1, x_2, x_3, eos]$，输入trg[:-1]，如“$<sos>$乘着风”，根据词表转化为4个向量的矩阵
加上位置信息
过Attention Mask了的Self-Attention
和没过Self-Attention的矩阵相加，然后LayerNorm标准化
得到的矩阵作为Q，Encoder矩阵作为KV，做Cross Attention
和没过Cross Attention的矩阵相加，然后LayerNorm标准化
过FFN，再和没过FFN的矩阵相加，然后LayerNorm标准化
过一层全连接和Softmax，得到$\text{output} = [y_0, y_1, y_2, y_3]$，例如得到“乘着车$<eos>$”
多分类问题用交叉熵计算trg[1:]和output间的损失、更新参数

Decoder推理时，这个流程变成：

向Decoder输入$<sos>$，输出$[y_0]$
合并得$[<sos>, y_0]$，继续向Decoder输入，得$[y_0^{'}, y_1]$
合并得$[<sos>, y_0, y_1]$，以此类推
当预测到$<eos>$，或者达到设置的最大长度，停止

通过本章，相信你已经对 Transformer 模型的定义和发展有了大概的了解。幸运的是，Hugging Face 专门为使用 Transformer 模型编写了一个 Transformers 库，并且在Hugging Face Hub中提供了训练好的模型以供快速使用。

在后面的章节中我会手把手地带你编写并训练自己的 Transformer 模型。